Duudel – AI Music Composition

Computers have already had a huge impact on all our lives: They do many tasks for us and make life a lot easier and yet they still have not been able to take over the creative side of life. Although computers are considered to be very powerful machines that can solve almost any algorithmic problem, they still are not trusted to make a painting, write stories, or indeed compose music.

But why should computer programs not do all of these wonderful things? Who are we to claim that only humans can make art as beautiful as we have seen in human history? Why should it not be possible for a computer program to be artistic and considered to be creative?

These are just some of the reasons that led Moritz Pflanzer and me to do more research in the field of algorithmic music composition. From the information we gathered and some of the ideas we had, we developed Duudel, an autonomous music composer that aims to use as few rules as possible to compose music that is pleasant to our ears and that can compete with human-made music.

Background and Current Research

Although the field of algorithmic music composition is still a relatively new area of research, there have already been quite a few reasonably good attempts to generate music with a computer. These include:

• Wolfram Tones, which uses a cellular automaton that composes music based on the 256 so-called elementary rules for cellular automata that Stephen Wolfram described in “A New Kind Of Science“
• Ludwig, which uses existing pieces of music to assemble them into something new
• Auto Music Composer Light (previously: http://www5f.biglobe.ne.jp/~mcs/amc.html), which composes short melodies based on chords that the user provides
• Computational Music Composition, the predecessor of Duudel that also used cellular automata and genetic algorithms to compose new pieces of music from a set of transition probabilities between notes

Although some of the existing projects produce acceptable results, none of them manage to compose music with very few rules whilst at the same time making music that can be mistaken as a piece composed by a human. This, however, is ultimately our goal:

To develop an autonomous music composer that uses as few rules as possible to compose music that can be mistaken as some that was made by a human.

In our previous project “Computational Music Composition” we had used a cellular automaton combined with genetic algorithms as the core of the composition algorithm. However, we found that although this concept gives us a great way to deal with the amount of data very efficiently and even lets us listen to reasonably good results, the model is not good enough when it comes to reducing the number of set rules the algorithm uses. Very few rules lead to very bad results.

This, we find, is due to the fact that although cells in the automaton can have different states and the states can “move around the board” this movement does not actually mean anything. This does not make sense to some extend, as music composition relies on the fact that notes and sequences of notes are related to each other in a meaningful way.

It turns out that Leonhard Euler provided the solution to this problem in 1739, when he described a so-called “Tonnetz” (Tonal Network), a grid of chords that describes the relationship between different harmonies and notes.

What is a Tonraum (Tonal Network)?

A Tonnetz in its simplest form can be represented as a grid of notes that. In order to understand the concept of the Tonraum, we shall consider the following example:

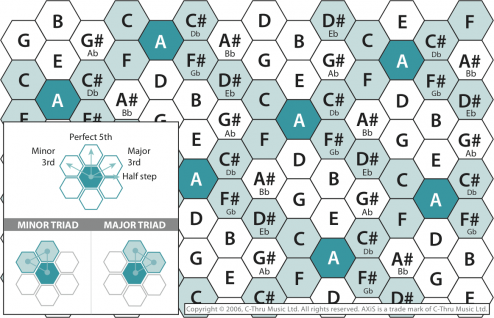
In the Tonraum, possible intervals are represented by the adjacent edges and corners. Interestingly we note that any three adjacent notes always result in a reasonable triad. In addition to this, we can even tell whether said triad is minor or major.

Design of Duudel

As discussed before, we use the concept of a tonraum to form the core of our program. There are two different versions of a tonraum: a flat grid as discussed before and one that can be represented as a torus, such that every note in the grid has the same number of neighbours.

The latter approach would mean that we would not have to consider the edge case when the composition (which is represented by moving around the board) reaches the end of the grid. This seems tempting because it allows the composition to choose from the same number of neighbours in every step.

However, a fundamental concept of the tonraum is that after any point in the process of the composition, there is only a set number of intervals that are allowed in the next step. It turns out that modelling the tonraum as a torus results in some disallowed intervals being composed, which cannot be fully explained by music theory – it does not make sense as a composer to chose such a disallowed interval.

Therefore, we choose the former approach and treat the edge cases as such.

Duudel actually supports many different versions of a tonraum. Each tonraum has different features, although the main characteristic of a tonraum is the way it chooses the next note. In order to simulate creative behaviour, we define probabilities for the next possible intervals. The way that these probabilities are constructed can vary between different tonraums.

For example, in tonraum A, each possible interval is associated directly with a transition probability. In tonraum B, however, we take into account the note that was last composed (Markov Chains).

Playing Music In a Specific Key

Although we can already play the music that Duudel composes, it is still very hard to follow and quite frankly not very pleasant at all. This is partly due to the fact that we need a way for the composition process to always take into account a specified key, say C major.

In order to achieve this, we use so-called “reference notes”. These notes consist of the key and are marked in the tonraum. In addition to the keynote, we use the notes from the first voice as reference notes for the second. This way, the first voice is influenced by the keynote, and the other voices are directly influenced by what the first voice plays. Thus, they are indirectly influenced by the keynote.

Furthermore, we use a weak version of a cellular automaton for the composition of the main voice: A certain number of previous steps are seen as states of the board, and are taken into account for the next step. The composition is then influenced such that notes close to accumulation points on the board are preferred. Accumulation points are points on the board that are surrounded by relatively many notes in the composition. This gives us the opportunity to actually play notes that are likely to complete, say, a triad.

Note that we always work with probabilities, which means that we can still get some rather dissonant sequences of notes. However, we see this as a benefit of our technique, since many famous works by famous composers also feature some dissonant parts, that actually make the piece interesting.

Remembering Sequences We Have Already Played

One very important feature of human-composed music is that each piece of music has a certain structure and some themes are repeated and altered as the song progresses. We therefore have to find a way to model this kind of behaviour.

This “music memory” can memorise sequences of notes, that is, sequences of pitches, note lengths, volume and accentuation. However, we find that simply memorising and then repeating those sequences later results in rather boring music. Instead, we want to be able to amend the newly-found themes slightly, as a human composer would: We can split the sequence into two at a particular point, transpose it by a given interval or simply change atomic parts of the sequence. This way, we can improve sequences that are at first not considered to be great by the listener.

Every sequence has an associated quality, which is defined as the sum of the quotients between the probabilities of the found interval and the best possible interval. In addition to this, before a sequence is repeated another function determines the quality of the sequence with respect to its current position in the piece:

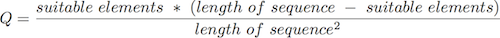
This formular describes a graph of a parabola which has its maximum exactly where the memorised note sequence matches half of the previously played notes. By dividing by the square of the length we standardise the quality so that we can compare sequences of different lengths.

Rhythm Is It!

Of couse, so far we have only been able to play different notes with the same length. We now have to find a way to deal with the composition of a suitable rhythm for the composition.

We define rhythm to comprise both the general structure (i.e. stanza, chorus, etc.) and the lengths of the individual notes that are to be played in that structure. While the general structure of a piece is described in exact terms as part of the definition of a specific rhythm module, the lengths of the notes are dependent both on the beat and the intervals that have already been played. For instance, in music theory, we find that great intervals often come with long notes, while small intervals are often played faster.

In addition to this, the rhythm of a piece is also influenced by the accentuation and volume of the individual notes. Although this is not integrated into the algorithm yet, we believe that it could be worth looking into crescendos and decrescendos when playing ascending, great intervals or descending, small intervals respectively.

The rhythm is often enforced by some sort of percussion instrument which leads us to include one in our composition. This actually improves the resulting music enourmeously.

In addition to the basic probabilities for note lengths, there are also some other factors that influence this part of the rhythm composition:

• Note grouping: In existing works, it often happens that notes of the same length follow each other and form a sort of rhythm block. This can, for example, be seen in Mozart’s “Klaviersonate in C-Dur” (KV 279).
• Consistency-boredom-principle: The more often a note length is repeated straight away, the more likely it is for the listener to find the music uninspiring or even boring.
• Interval-length-correlation: Great intervals often come with long notes, while small intervals often appear with short notes.
• Bar-filling: For reasons of simplicity, we want to compose full bars at the moment. This means that a note cannot span over several bars, which in turn means that composing the contents of one bar should be done in a way that allows easy completion of that very bar.

In the program, we define mathematical functions to model all of these four behaviours.

Conclusion

Putting all of the described techniques together, we actually get a rather good result. The resulting music is acceptable and even though some of the patters seem unnatural and random we managed to produce a music composition tool that composes music using very few rules.

Feel free to listen to some sample compositions:

• Sample 1
• Sample 2
• Sample 3

Note: This is a revised version. The original article was published in 2012.